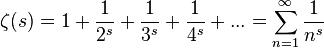リーマンのゼータ関数を描画してみた

数々の数学者の人生を狂わせたリーマン予想というものがある、ということは以前から知識として知ってはいたのですが、とあるキッカケでなんとなくWikipediaで調べてみました。

ゼータ関数を次のように定義する。
$http://upload.wikimedia.org/math/3/c/2/3c295b03578ef959e080c322d9682ee0.png$
1859年にリーマンは自身の論文の中で、複素数全体 (s ≠ 1) へゼータ関数を拡張した場合、
ζ(s) の自明でない零点 s は、全て実部が 1/2 の直線上に存在する。
と予想した。
リーマン予想 - Wikipedia

あーそういえば数学ガールでバーゼル問題は読んだなあと思いつつ、難しいことはサッパリ分からんが正月休みのヒマを埋めるべくとりあえずゼータ関数を可視化してみたら面白いかもしれんと、プログラミングの書き初めを始めたわけであります。

まずゼータ関数に出てくる数列を次のように定義します。（あ、C#ね）

    static IEnumerable<Complex> ZetaSequence( Complex z )
    {
      int n = 1;
      while ( true ) yield return 1.0 / Complex.Pow( n++, z );
    }

.NET Framework 4.0 から Complex 型が導入されたので大変便利ですなー。
次にこの数列の和を計算してゼータ関数が定義されます。

    static Complex ZetaFunc( Complex z )
    {
      const int N = 1000;
      return ZetaSequence( z ).Take( N ).Aggregate( Complex.Zero, ( acc, item ) => acc.Magnitude < 10.0 ? acc + item : acc );
    }

ここでは数列の1000項まで計算することにしました。あと、無限大に発散されても困るので絶対値10未満に抑えました。

ここからゴニョゴニョと色々やって、OpenGLで描画したものがこちら。
f:id:u_1roh:20130102194550p:plain