かたちづくり

つれづれに、だらだらと、おきらくに

波の干渉を可視化してみた

現在、四苦八苦しながらファインマン物理学2巻を読んでいるのであります。

ファインマン物理学〈2〉光・熱・波動

ファインマン物理学〈2〉光・熱・波動

今のところ1/3くらいは読んだかな…？ファイマン先生が舌鋒鋭く光の屈折の本質に迫っていく辺りに感動を覚えつつも、まあ、消化不良ですね。それはともかく、波の干渉の様子をOpenGLで可視化できたら面白いかもしれんなどと思いましてプログラムを書いてみました。本当は屈折の原理に感動したので屈折をシミュレートするプログラムが作ってみたかったのですが、ちょっと考えただけでも難しそうだったのでそれはあっさり諦めました(^^;

まず波源を定義します。

type WaveSource = {
    Position  : Point2d
    Amplitude : double
    Lambda    : double
  }

Point2d の定義は書いてありませんが、名前から想像がつく通り2次元の点座標です。2次元平面上の点と振幅（Amplitude）、波長（Lambda）によって波源が定義されます。
次に、複数の波源から構成される「場」を定義します。

type WaveField = {
    WaveSources     : WaveSource list
    FieldSize       : Size2i
    FieldOrigin     : Point2i
    LengthPerPixel  : double
  }

Size2i は整数値による2次元のサイズ（つまり幅と高さ）、Point2i は整数値による2次元座標です。離散化された2次元のグリッド上に波を発生させてそれを可視化しようというわけです。ですのでグリッドのサイズやら解像度やら原点位置やらを表すフィールドが並んでいます。
次に示すのは一つの波源が発生させる波を表す関数です。

let private evalWaveSource source (p : Point2d) =
  let r = (p - source.Position).Length
  let k = 2.0 * Math.PI / source.Lambda
  source.Amplitude * (if r < 1.0e-6 then k else sin (k * r) / r)

source は WaveSource 型の波源です。この関数は波源 source が位置 p に起こす波の振幅を返します。特異点のゼロ割を回避するコードを除けば、三角関数によるシンプルな波であることが読み取れるでしょう。

単純な一つだけの波源

まずは単純に、波源を一つだけ置いて可視化してみます。
http://i.gyazo.com/81b2ce1703de69fa86b03aa2387ee2d0.png
場は次のように定義しました。

{ WaveSources = [{ Position = Point2d (0.0, 0.0); Amplitude = 400.0; Lambda = 20.0 }]
  FieldSize  = Size2i( 512, 512 )
  FieldOrigin = Point2i( 256, 256 )
  LengthPerPixel = 1.0 }

描画はOpenGLで行っていますが、独自ライブラリを使っていますしコードもやや煩雑なので説明は省きます。
※ 振幅やら波長やらは見た目が良い感じになるように調整しただけですので特に意味がある数値ではありません。

指向性のある波源

今度はX軸上に複数の波源を並べてみたものです。波長よりも短い間隔で波源が並べられていることがミソです。こうするとY軸方向に指向性のある波が生成されるとのことですが…。
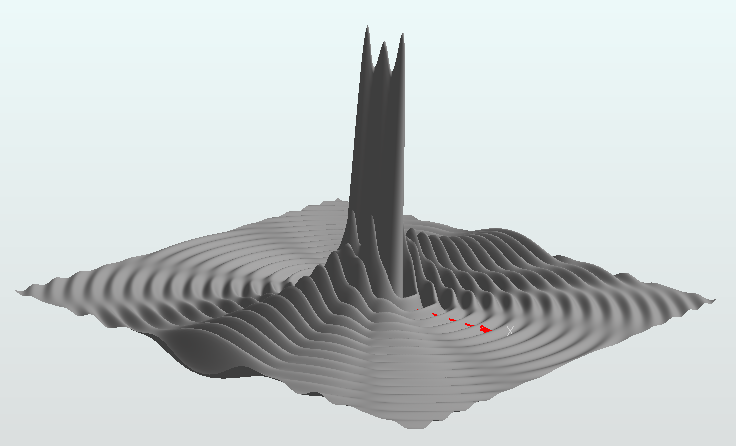
http://i.gyazo.com/c9d8019141d3e007db967c3a03e01f19.png
X方向から見た図（つまりYZ面）。
http://i.gyazo.com/1c62c0a58cecc9dc2bae14425ea62fcb.png
Y方向から見た図（つまりXZ面）。
http://i.gyazo.com/9f512e282a81d3354394354601cd2269.png
おおー、確かにY軸方向に指向性が現れています。Y軸上では全ての波源の位相が一致するので互いに強め合って波が遠くまで伝送されますが、それ以外の方向へは位相がズレるため互いに打ち消し合ってしまい、波は伝送されません。
場は次のように定義しました。X軸上に 5.0 間隔で波源が13個並んでいます。

let waveSource x =
  { Position = Point2d (x, 0.0); Amplitude = 400.0; Lambda = 20.0 }
let sources =
  [0.0; 5.0; -5.0; 10.0; -10.0; 15.0; -15.0; 20.0; -20.0; 25.0; -25.0; 30.0; -30.0]
  |> List.map waveSource
{ WaveSources = sources
  FieldSize  = Size2i( 512, 512 )
  FieldOrigin = Point2i( 256, 256 )
  LengthPerPixel = 1.0 }

干渉縞を作る波源

最後は、有名な干渉縞を作る場のシミュレーションです。波源の塊を少し離れた位置に2つ配置しています。
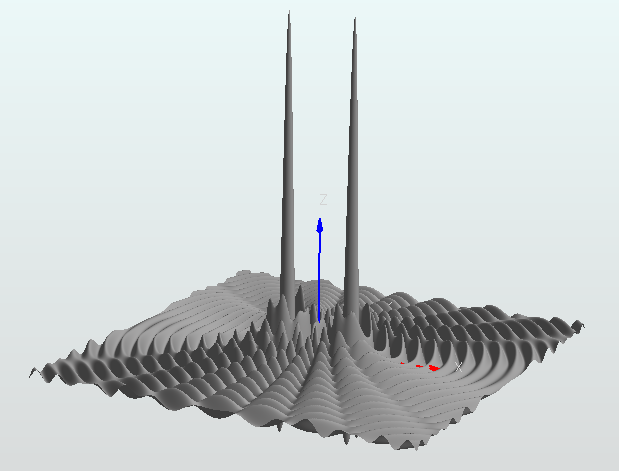
http://i.gyazo.com/c3849ef05eee2dacea2e4fc667664ae2.png
学校の授業でレーザー光をスリットに当ててスクリーンに干渉縞を投影した実験が懐かしいです。場は次のように定義しました。2つの波源の塊が 80.0 の間隔を空けて並んでいます。これが二重スリットを通り抜けた2つの光源をシミュレートしています。

let waveSource x =
  { Position = Point2d (x, 0.0); Amplitude = 400.0; Lambda = 20.0 }
let sources =
  [ waveSource 40.0; waveSource -40.0
    waveSource 43.0; waveSource -43.0
    waveSource 46.0; waveSource -46.0
    waveSource 49.0; waveSource -49.0 ]
{ WaveSources = sources
  FieldSize  = Size2i( 512, 512 )
  FieldOrigin = Point2i( 256, 256 )
  LengthPerPixel = 1.0 }

以上、単に複数の波を重ねあわせただけの単純な実験ですが、ちょっと楽しいですね。